That’s a harsh statement, and quite opinionated you may be thinking! But wait, hear me out as I try and make my case.
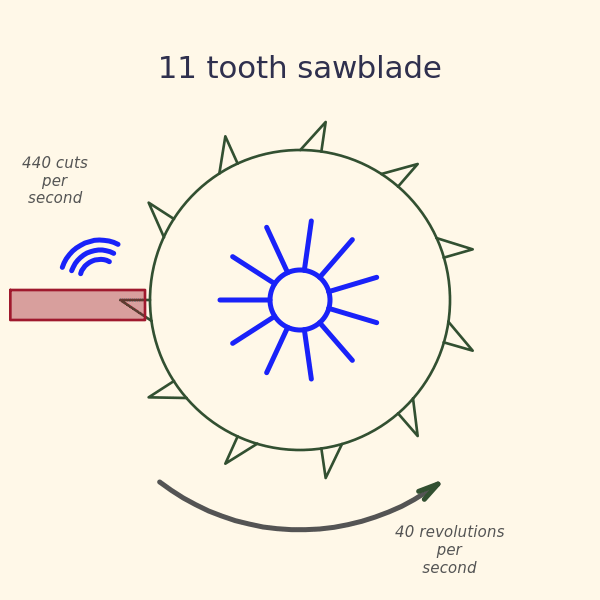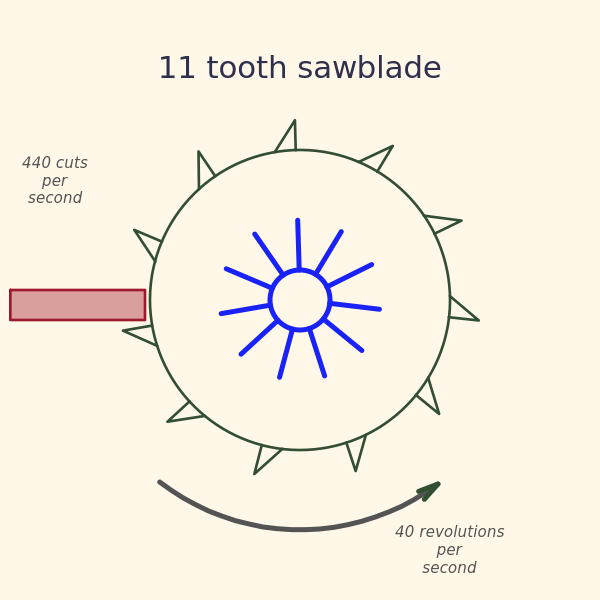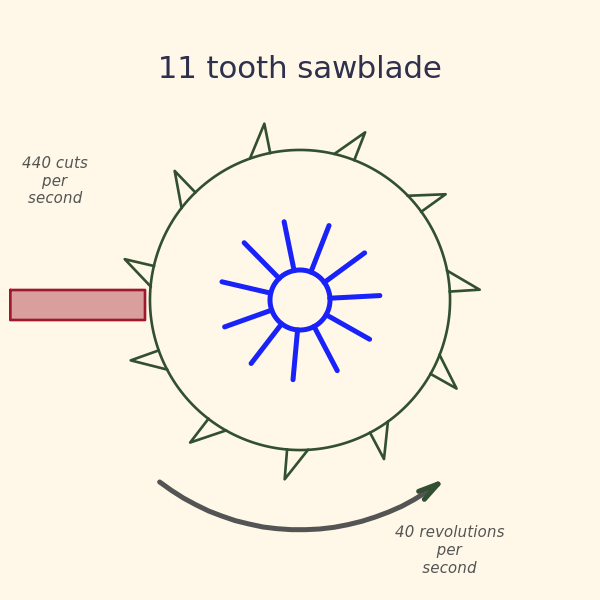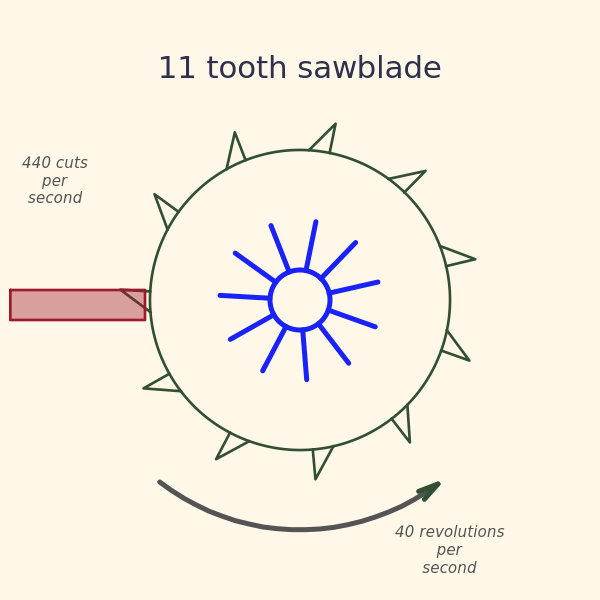
Let’s start with what is sound? A sound can be characterized primarily by its frequency. What does that mean? Is it some abstract property like the frequency of the WiFi signal you’re connected to, or the frequency of radio station? Quite to the contrary! The frequency of sound has a very simple physical interpretation. All sound emanates from some kind of mechanical vibration of something hitting, scratching, or scraping something else. Take for example the saw blade in the picture below. It has 11 teeth located around its perimeter, and is turning at a speed of 40 revolutions per second. This means that a tooth is hitting the piece of wood 440 times per second. This just happens to be the precise frequency of the musical note “A”, and if you were standing next to this saw, you’d hear a perfectly tuned “A” buzzing its way thru the piece of wood.
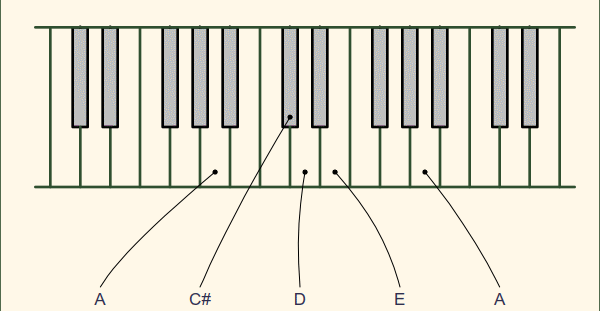
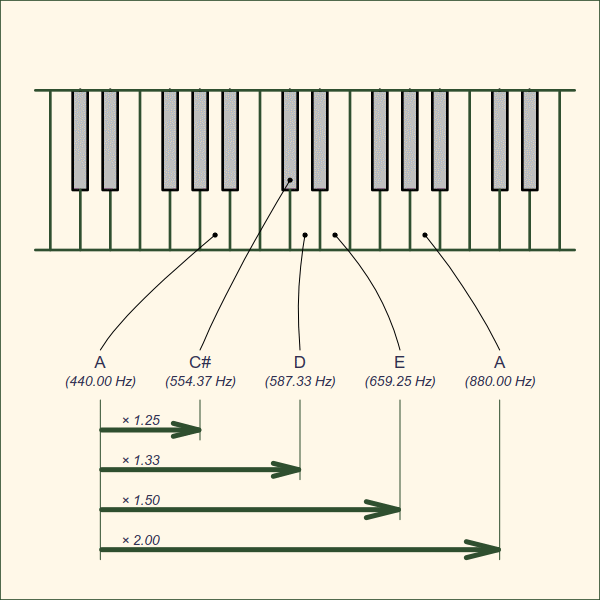
This is the same pitch that you’d hear if you walked by a piano, and hit the “A” key as pictured below, or plucked the “A” string on a violin. Other keys have a higher pitch, and correspond to a higher frequency.
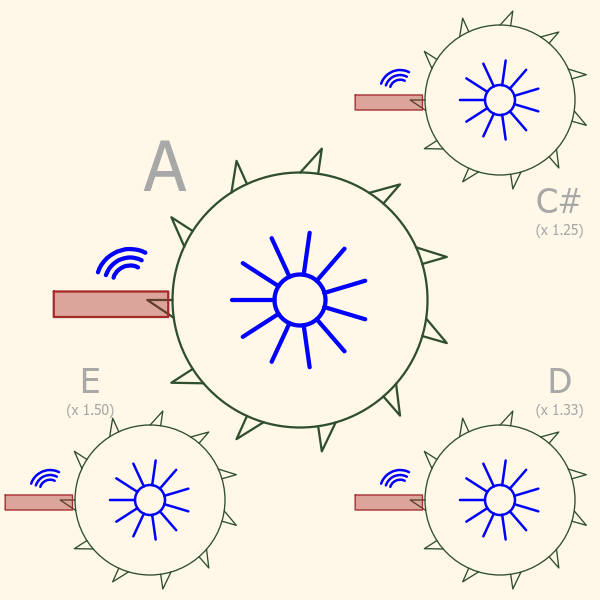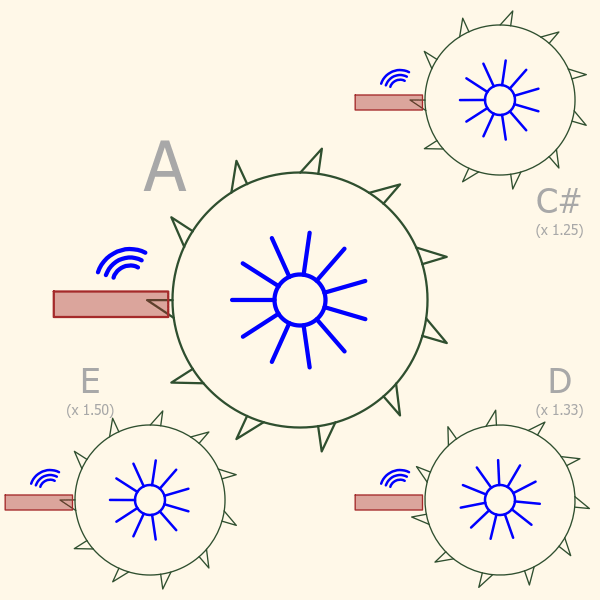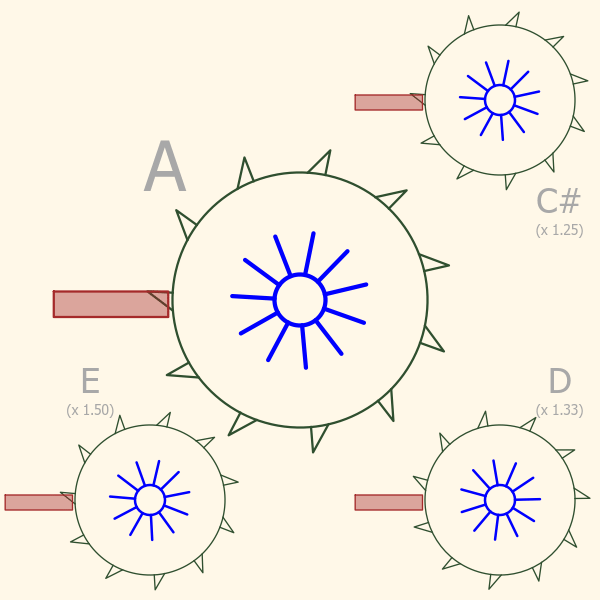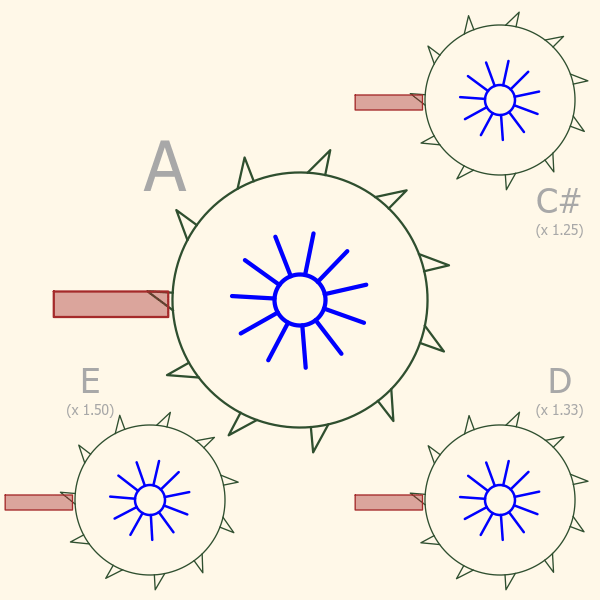
If you look at the third picture below, here’s where it really gets interesting! The large saw blade in the middle is still spinning the the same speed as before, generating a perfectly pitched “A”. Each smaller blade is spinning slightly faster, generating higher frequency sounds.
Notice the little sound bursts coming off each of the saw blades. They are all happening at different rates, yet you can easily see that some that are “in sync” with each other, while others seem not to be. Actually all the blades are in sync with each other, its just that some have simple ratios, and others more complex ratios. The easiest to see this on is “A” and “E”. Every third sound burst coming off the “E” saw blade aligns with every second burst coming off the “A”. This happens because their frequencies have a simple ratio of 3-to-2, or (3/2). If we list all the possible pairs you can make from these four notes we have :
| A + E | 3/2 | Great! |
| A + D | 4/3 | Good |
| A + C# | 5/4 | Pretty Good |
| C# + D | 16/15 | Terrible |
| C# + E | 6/5 | ok |
| D + E | 9/8 | Bad |
As you might have guessed, the third column is how good the two notes sound when played together.
There’s something really interesting going on here! The pairs of saw blades whose relative speeds can be expressed as the ratio of two small integers (like 4/3 or 3/2) are very synchronized, and they sound good when played together. Pairs that don’t have a simple ratio “clash”!
We can even take this one step further and play three notes at the same time like (A + C# + E) or (A + D + E). All of the notes in the first trio (A + C# + E) sync well with each other, and all three together produce an even more rich complex sound we call an A-major chord. If we try and do the same thing with (A + D + E), it sounds like something breaking. That’s because the “D” and “E” just don’t sync up nicely. They have a frequency ratio of 9/8, so only 1 out of every 9 sound bursts from the “E” saw blade aligns with a sound burst from the “D” saw blade. That’s just not enough alignment to sound good.
Hopefully it’s clear now – sound is characterized by its frequency, and when the frequencies of two or more sounds occur in simple integer ratios like 3/2, 4/3, or 5/4, they beat together nicely and form very pleasing complex sounds and harmonies we all love to hear.
So there you have it, something for everyone. For the left-brained math types, there’s the integer ratios of frequencies within a chord that form perfect resonances, and for the right brained art/music types there’s the deep appreciation for the infinite ways in which the notes of various pitches can be combined and sequenced to create the music that is such a vital part of our history and culture.
I wish that were the whole story and we could just end it there, but sadly we can’t. Just like life itself where it seems like the longer you live, the more you find out things you thought were simple, aren’t so simple after all. So it is with music, notes, and harmony.
Here’s the problem : if “A” is precisely 440.0 Hz, then for perfect resonance, “D” should be exactly a factor of 1.5 times higher (3/2) in frequency, and thus the frequency of “D” should be 660.0 Hz. Why is “D” listed as 659.25 Hz in the keyboard picture above? (and if you look up the frequency of “D” on google, it will say 659.25 Hz too!) What’s going on here? If “A” is 440 Hz, then the best frequency to resonate with it would be 660.0 Hz, not 659.25 Hz.
The discrepancy here comes from the fact that our music scale divides each octave into 12 “equally” spaced notes, like the 12 keys on a piano keyboard between one “A” at 440 Hz and the next “A” in the adjacent octave at 880 Hz. In order to get to exactly a factor of 2.0 in 12 equal steps, the frequency of each adjacent note is raised by a factor of 1.059463094… or 21⁄12. Sadly, like π, this is an irrational number, going on forever. When you create a music scale based on this irrational scaling ratio, it’s surprising music even works at all!
And yet it does! Whoever picked 12 to be the number of notes to span an octave knew what they were doing! 21⁄12 turns out to be an amazingly good geometric spacing such that many notes land remarkably close to the ideal ratios of 3/2, 4/3, and 5/4, but nevertheless they’re slightly off. Even an untrained ear can hear the difference when two notes on or off perfect resonance by even a fraction of a percent.
When playing a fixed note instrument like a piano, the frequency locations of each note is preset, and can’t be adjusted on the fly. Other instruments like the violin, and even human voice can ever-so-slightly adjust the pitches of some notes within a chord to bring them into perfect resonance.
It turns out our music scale with its 12 notes per octave irrationally yet evenly spaced across an octave is not perfect, but close enough!